¿Que es la geometría analítica?
Se conoce como geometría analítica al estudio de ciertas líneas y figuras geométricas aplicando técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.
o novedoso de la geometría analítica es que permite representar figuras geométricas mediante fórmulas del tipo f(x, y) = 0, donde f representa una función u otro tipo de expresión matemática.
La idea que llevó a la geometría analítica fue: a cada punto en un plano le corresponde un par ordenado de números y a cada par ordenado de números le corresponde un punto en un plano.
Fue inventada por René Descartes y por Pierre Fermat, a principios del siglo XVII, y como vimos, relaciona la matemática y el álgebra con la geometría por medio de las correspondencias anteriores.
Además, Descartes y Fermat observaron, y esto es crucial, que las ecuaciones algebraicas corresponden con figuras geométricas. Eso significa que las líneas y ciertas figuras geométricas se pueden expresar como ecuaciones y, a su vez, las ecuaciones pueden graficarse como líneas o figuras geométricas.
En particular, las rectas pueden expresarse como ecuaciones polinómicas de primer grado y las circunferencias y el resto de cónicas como ecuaciones polinómicas de segundo grado.
Distancia entre dos puntos
Cuando los puntos se encuentran ubicados sobre el eje x o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas.Ejemplo: La distancia entre los puntos (-4,0) y (5,0) es 4 + 5 = 9 unidades.
Cuando los puntos se encuentran ubicados sobre el eje y o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.
Ahora si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:
Para demostrar esta relación se deben ubicar los puntos A(x1,y1) y B(x2,y2) en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa AB y emplear el teorema de pitágoras.
Ejemplo: Calcula la distancia entre los puntos A(7,5) y B (4,1)
d = 5 unidades
punto medio:
Ejemplo
Hallar las coordenadas del punto medio del segmento AB.
pendiente:
La pendiente de una recta en un sistema de representación rectangular (de un plano cartesiano ), suele ser representado por la letra  , y es definido como el cambio o diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta. En la siguiente ecuación se describe: toda recta que no sea horizontal, tiene que cortar al eje "x". se dice que si una recta corta al eje X, la inclinación de la recta se define como el ángulo positivo menor de 180°.
, y es definido como el cambio o diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta. En la siguiente ecuación se describe: toda recta que no sea horizontal, tiene que cortar al eje "x". se dice que si una recta corta al eje X, la inclinación de la recta se define como el ángulo positivo menor de 180°.
 , y es definido como el cambio o diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta. En la siguiente ecuación se describe: toda recta que no sea horizontal, tiene que cortar al eje "x". se dice que si una recta corta al eje X, la inclinación de la recta se define como el ángulo positivo menor de 180°.
, y es definido como el cambio o diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta. En la siguiente ecuación se describe: toda recta que no sea horizontal, tiene que cortar al eje "x". se dice que si una recta corta al eje X, la inclinación de la recta se define como el ángulo positivo menor de 180°.[editar]Geometría
Una recta horizontal tiene pendiente igual a 0 (cero). Cuanto menor sea el valor de la pendiente, menor inclinación tendrá la recta; por ejemplo, una recta que se eleve un ángulo de 45° con respecto al eje X tiene una pendiente m = +1, y una recta que caiga 30° tiene pendiente m = -0,5. La pendiente de una recta vertical no está definida, o se dice que es infinita.
El ángulo θ que una recta forma con el eje horizontal está relacionado con la pendiente m por medio de la siguiente relacióntrigonométrica:
o equivalentemente:
Dos o más rectas son paralelas si ambas poseen la misma pendiente, o si ambas son verticales y por ende no tienen pendiente definida; dos o más rectas son perpendiculares (forman un ángulo recto entre ellas) si el producto de sus pendientes es igual a -1.

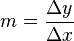


me parece que esta bien echo y se entiende.
ResponderEliminar